Solving Absolute Value Equations: A Basic Introduction to Algebra
Learn how to solve absolute value equations using simple algebraic steps and find the possible values of x.
00:00:01 Learn how to solve absolute value equations and find the possible values of x using simple algebraic steps.
✨ The absolute value always produces a positive result.
🔢 The absolute value of a number can be the number itself or its opposite.
📝 Absolute value equations can be solved by considering both positive and negative solutions.
00:01:06 Learn how to solve absolute value equations by writing two equations and finding the solutions for x. Apply the same method to solve another equation.
🔑 To solve absolute value equations, you need to write two equations: one with the positive value and another with the negative value.
🔍 By solving both equations, we can find the solutions for the variable x.
✨ In the examples given, the solutions for x are 7 and -11, and 3 and 4, respectively.
00:02:10 Learn how to solve absolute value equations in this basic introduction to algebra. Understand the concept and find solutions.
Absolute value equations involve the absolute value function.
Solving absolute value equations involves checking the equation for different values of x.
Absolute value equations can sometimes have no solution.
00:03:12 Learn how to solve absolute value equations by isolating the absolute value function and creating two equations. Solve for x.
⭐ Absolute value equations can only equal zero or a positive number.
✏️ To solve absolute value equations, isolate the absolute value function and write two separate equations.
🔢 Solving for x in the given example, x can be equal to four or negative two.
00:04:14 Learn how to solve absolute value equations in this basic introduction to algebra.
🔍 Solving absolute value equations involves finding the value(s) that make the equation true.
✏️ To solve absolute value equations, isolate the absolute value expression and solve for both the positive and negative cases.
✅ Check the solution(s) obtained by substituting the value(s) back into the original equation.
You might also like...
Read more on Education
La Reforma Educativa en 8 minutos

Ontario Tech - BA Pathways (Upgrade Your University Degree)

Student-Centered Learning: Building Agency and Engagement
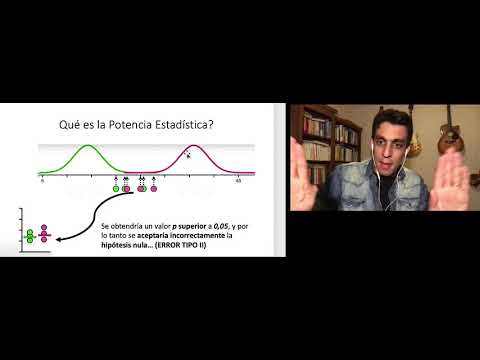
potencia estadistica y tamaño del efecto
Perplexity AI: The Answer To Any Question?
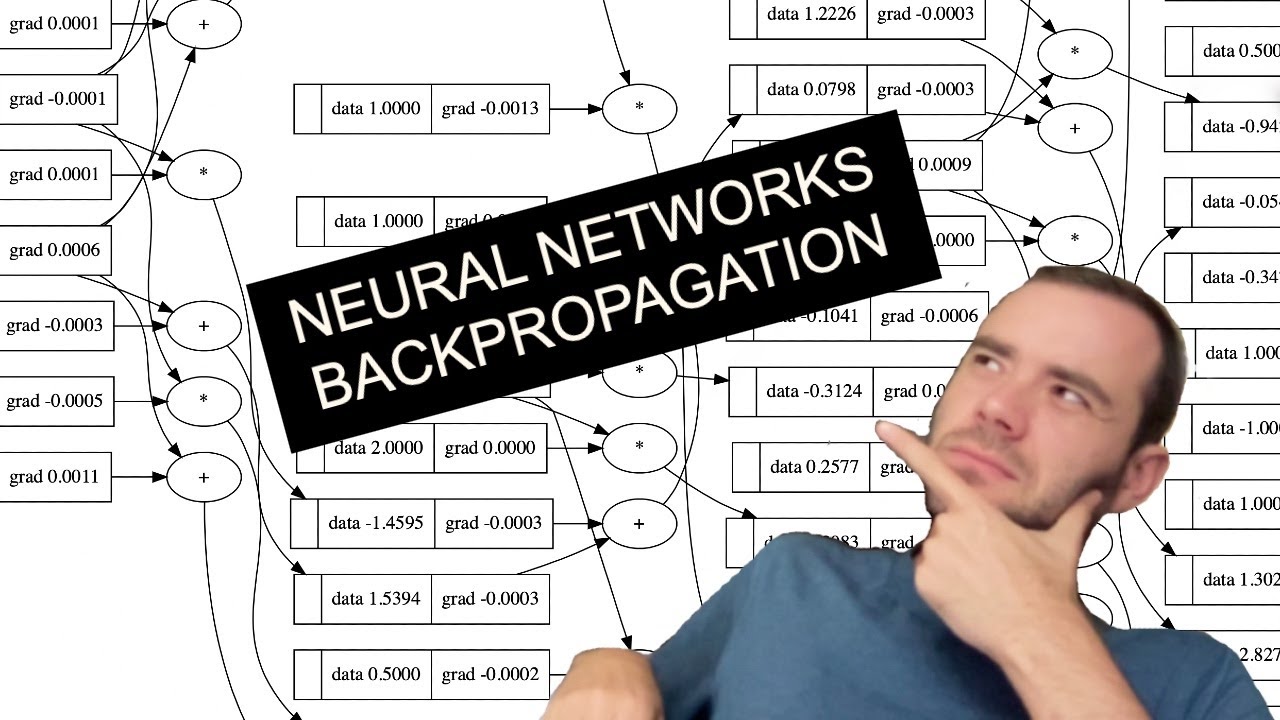
The spelled-out intro to neural networks and backpropagation: building micrograd